高中函数,是高中数学课程中非常重要的一部分,每年高考数学都会涉及函数相关的计算与运用。学生在学习函数的过程中,能够打破思维定势,提高计算能力,对事物有着更为清晰的认识。使用思维导图,可以帮助学生党更有效的学习、理解函数知识点。
函数至今,已有300多年的历史。早在十七世纪,伽利略在《两门新科学》一书中,用文字和比例的语言表达函数的关系,可谓是函数的早期身影。而后,牛顿、莱布尼兹建立了微积分;约翰·贝努利定义了函数的概念;叶欧拉、豪斯道夫等数学家在前辈的基础上不断完善函数的定义。数学家们从集合、代数等角度不断赋予函数新的概念与思想,有效地推动了整个数学的发展。
构建高中数学思维导图
函数的内容复杂而又繁多,不便于记忆。通过思维导图软件,我们可以梳理函数知识,构造函数体系。从概念、性质和微积分三个角度出发,整理出以下的思维导图。
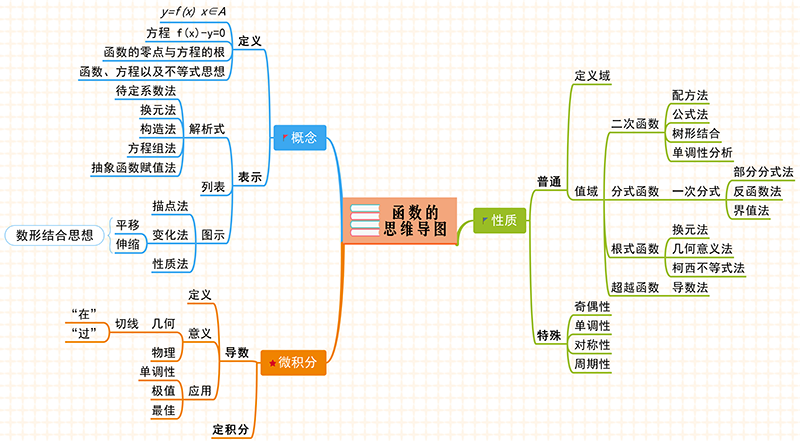
高中函数思维导图
高中的函数,重要的部分有6个,介绍如下:
- 一次函数:在某个变化过程中,设有变量x和y,将其写成y=kx+b(k是一次项系数,且不等于零,b是常数),则y是x的一次函数,并且x是自变量,y是因变量。
- 二次函数:二次函数的基本形式是:y=ax²+bx+c,二次函数的图像是一条对称轴平行或者是重合于y轴的抛物线。
- 指数函数:形如y=a^x(a>0且a≠1)(x∈R)的函数称为指数函数 。
- 对数函数:如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数。
- 幂函数:形如y=xa(a为常数)的函数。
- 三角函数:三角函数是以角度为自变量,角度对应任意两边的比值为因变量的函数叫三角函数,常见的三角函数包括正弦函数、余弦函数和正切函数。
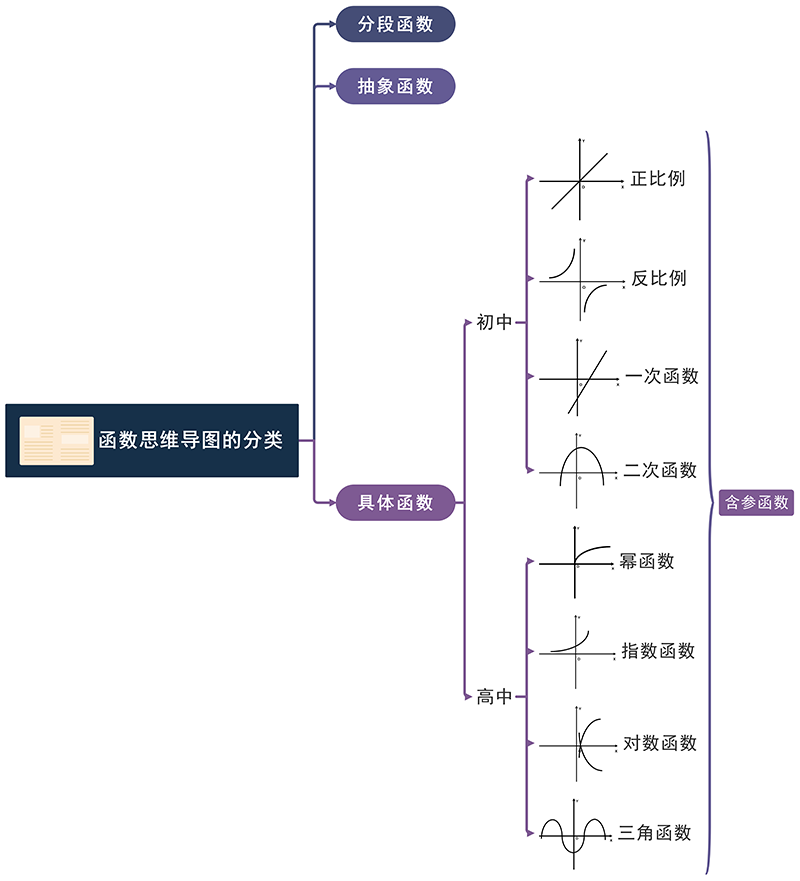
上述思维导图可以清晰地表达中学函数的分类与图像。有助于我们理解与记忆。
总而言之,不论知识点有多么的复杂与抽象,都可以将知识拆分出来,做仔细的分析与研究;再利用思维导图将所有知识点进行关联,不断完善知识。在这一个过程中,核心的技能是要掌握思维导图的用法。你可以下载MindMaster思维导图软件,再通过专业的思维导图教程,学会这项本领。
温馨提示:>> 点击进入思维导图社区,搜索:函数,即可免费获取本文高清版思维导图。
更多经典思维导图高清模板,欢迎在线搜索查看!








